
 manta ray
manta ray
June 2022
Level 3: Generating random numbers in GameMaker
Now that we've covered the essentials of PRNGs, we will start using GameMaker's built-in random number generator, understanding the different functions available and exploring possible pitfalls.
Generating (discrete uniform) random numbers
We'll start by generating a uniform random integer within a range. Say, for example, we need to simulate a fair six-sided die roll. We can use irandom_range function:
die_roll = irandom_range(1,6);
As you can see, this function expects two integers and generates discrete uniform random numbers within that range (inclusive), and returns an integer. Simple, right? There is also an irandom function, which takes a single integer and generates values between 0 and that number, so our die roll could also be generated like so:
die_roll = irandom(5) + 1;
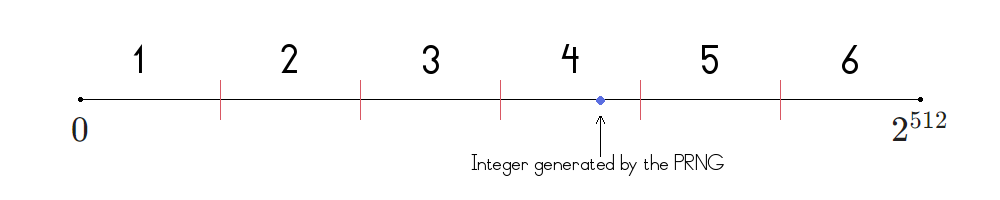
Perhaps you're wondering how would the PRNG generate a number between 1 and 6 (or 0 to 5), if the PRNG naturally produces values between 0 and $2^{512}$. The key here to remember is that numbers are independent and identically distributed (i.i.d.). Hence, all six values have the same probability, and so we can perform the following trick:
- Divide the period length into a number of "bins" of equal length. In this case, divide it into six bins of $2^{512}/6$.
- Assign the required numbers to each of the bins, consecutively. In our case, the first bin would represent the number 1, the second bin the number 2, etc.
- Make the PRNG naturally generate an integer (in our case, between $0$ and $2^{512}$).
- Select the number assigned to the bin in which the generated integer falls.
We can visually appreciate the method here:
This is what software does under the hood to generate arbitrary integer intervals or even $N$ different values. Think for example about randomly generating an arbitrary letter or game sprite; if you see, we can apply the same exact "bin" method to do it. Again, GameMaker we can already do this with built-in functions. For example, we can do:
genres = ["Action RPG", "Roguelite", "Simulation", "Platformer", "Sports"];
var _n = array_length(genres);
selected_genre = genres[irandom_range(0, _n-1)];
When distribution is unfirom we can also do this using GameMaker's choose function. It takes an arbitrary number of arguments (even if they're not the same data type!) and outputs a randomly selected one:
selected_genre = choose("Action RPG", "Roguelite", "Simulation", "Platformer", "Sports");
selected_sprite = choose(spr_Player_1, spr_Player_2, spr_Player_3);
The random seed
Before continuing to generate other types of random numbers, it is important to make sure we apply our knowledge of PRNGs obtained at earlier levels to this end. We know that all our pseudorandom number sequence depends on the seeded value. Hence, understanding how to manage the seed is key. The first thing to understand is that, if we don't explicitly tell GameMaker to do something specific with the seed, it always initializes the PRNG with seed 0 at the start of the game. This is a wise decision, since you would not want GameMaker to change the seed every time you compile your game. That would cause you to be unable to tell if your bugs are due to a specific realization/run of the PRNG or due to faulty game logic.
Notwithstanding, we also want to have control over our seeds. For testing, we want to initialize the PRNG to specific control values; for production builds, we generally want the PRNG to be initialized to a different value each time. To this end, we have some functions that we can use. First, let's introduce random_get_seed, which will allow us to know and store the seed of the current run of the PRNG:
seed = random_get_seed();
The seed will always be a 32-bit integer. We can use this value later to replay a particular level, or to save it along with the game's save data and be able to redraw the randomly-generated world whenever we load it back. To this end, we can take advantage of the related function random_set_seed, that takes a 32-bit integer as an argument and initializes (or resets) the PRNG with that value:
random_set_seed(1234);
Finally, if we need GameMaker to initialize (or reset) the PRNG with a different value each time, we could either come up with a "fancy" way of generating a seed, or use a built-in function. In the first case, we could, for example, set the seed to an integer value constructed with the date and time of the system. This way, every second we'll have a different seed and, thus, we'll be able to generate different pseudorandom values. Let's try it the hard way first:
var _x = date_current_datetime();
var _y = date_get_second_of_year(_x);
var _seed = round(_x)-44000 + _y;
random_set_seed(_seed);
show_debug_message("Seed is now "+string(random_get_seed()));
Since date_current_datetime returns the date and time of the system as the fractional number of days elapsed since January 1st, 1900, we can construct a positive integer value less than $2^{32}$ with it and use it as seed (here, I'm substracting 44,000 from the datetime value, because right now we're ~44,000 days after said date, so we want the day to modify the total value of the seed, but make the seconds play more, in order to have a different seed each time). Take note, if you use date_current_datetime directly, since it's a real number, GM will floor it (i.e. truncate the decimal part) before assigning the seed, so this will probably not result in what you expect (all runs on the same day will result in the same PRNG sequence!).
You could think on different (and better) ways to generate the seed, and there are other crazier methods of generating a random seed (such as polling the mouse movements) or you could even generate the seed using another PRNG (!), but let's stick instead to GameMaker's built-in way: the randomize function. We can call this to reset the PRNG to a different seed every time, much like the code above:
randomize(); // or randomise()
I couldn't find documentation, nor deduce, the exact way randomize assigns the seed, but it's probably either based on the computer's date and time, or it's being generated randomly. Either way, it's a good way of initializing the seed to a different value every time you run the game.
Once the seed is set (either automatically to 0 at game start, or to a random or concrete value using any of the functions above), GameMaker will not reset it unless we tell it to. This includes calling the game_restart function (one more reason using that function is not recommended unless you know its limitations and inner workings), so this is something to consider. Also, unless you specifically need to reset the PRNG, don't call randomize or random_set_seed (i.e. don't place them in a Step event, for example!), otherwise you'll be constantly reinitializing the pseudorandom number generator and you will not have the expected result.
Also, take into account, as discussed in the previous level, that HTML5 will not behave the same, since it's based on a different PRNG. So if you need the exact same output for a given seed on all export platforms, your best bet is to implement a custom PRNG yourself.
You can play with the following GameMaker app. Click on the die to roll it; click on the Reset PRNG button to reset the seed to 0 (remember this is the value GM initializes the seed to, at the start of the project). Click on the game_restart button to call that function. Finally, click on Actually Restart to manually reset the roll sequence as well as the seed. You can see for yourself that the sequences restart on each reset of the PRNG and that game_restart does not reset the seed.
Generating (continuous uniform) random numbers
As seen in the previous level, we can generate numbers between 0 and 1 by generating integers and then dividing by period length. However, GameMaker has an equivalent built-in function for simulating a random range. Guess what's it called? random_range, which takes two arguments and generates a continuous uniform variable:
value = random_range(0,1);
Analogous to the discrete case, we also have random that takes just one real and generates a continuous uniform value between 0 and the selected number. Also, with random_range we can generate values between any arbitrary real numbers by changing the parameters; please note that this is equivalent to the following function:
function manta_random_range(_a, _b) {
return _a + (_b-_a) * random(1);
}
This technique is called transformation of random variables: we use the output of one probability distribution and perform mathematical operations on them to generate new distributions. As we'll see later, turns out we will be able to generate most probability distributions with this trick.
Generating non-uniform finite discrete distributions
Now we're getting to the interesting part. Say we want to randomly decide what loot a player gets when they open a chest on our roguelite. We have the following options:
- 5 gold coins
- A +10 Sword of Cold, that freezes the enemy for 5 seconds
- A small health potion
- An Amulet of Mana, that increases mana by 2
We probably don't want to generate the loot uniformly, because we don't want the magic sword to pop out $1/4$ of the time! Similarly, we might want the amulet to be less likely to appear than the gold coins. In fact, this is the case for the majority of uses: uniform distributions do not model reality very well.
How could we generate a "weighted" distribution like that? Let's assign some probabilities to each possible loot item. Say we want the coins to generate 40% of the time, the health potion 30% of the time, the amulet 20% of the time and the sword 10% of the time. As we saw on the first level, our probabilities need to be nonnegative and add up to 1. Hence, one way of thinking about this is picturing these probabilities in the $[0,1]$ interval, as follows:
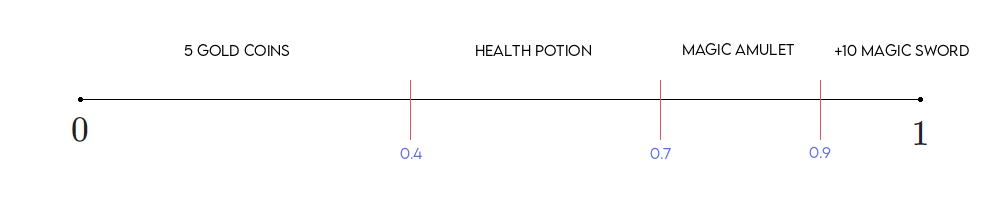
We can see the probabilities drawn on the number line. Now, let's think we generate a continuous uniform random number with our PRNG. Note that, if we once again check what bin does that number fall into, we'll be able to generate items with that probability. To understand the above, note that, for our number $n$ to fall in the coins bin, it needs to satisfy $n \leq 0.4$; for it to fall in the health potion bin, it needs to satisfy $n > 0.4$ and $n \leq 0.7$; and so on. This observation is all we need to create the algorithm that lets us generate numbers with the above probabilities:
- Create an array $A$ with the wanted items/names/values we want to select from.
- Create an array $P$ with the corresponding selection probabilities. Make sure the probabilities are nonnegative and add up to 1.
- Generate a single continuous uniform random number $n$ from our PRNG.
- Initialize our target "bin" (the array index) to 0.
- While $n$ is less than or equal than the cumulative sum of the probabilities up to (and including) the current bin, increment the target "bin".
- Return the item corresponding to target "bin".
Note our algorithm will always finish, provided probabilities add up to 1. We don't want probabilities to add up to 0.999, since our number $n$ can be 0.9991 and our while loop will not end.
I've written a utility function to implement the above algorithm. If both arrays are specified however, it implements the above algorithm and generates random items from $A$ with the specified probabilities $P$. It can return the item itself (default) or the index of the item in array $A$:
///@function array_random(array=[], probabilities=[], return_index=false)
///@description selects an index from the array with the specified probabilities
///@param {array} _array the array that holds the values to select from
///@param {array} _probabilities the array that holds the corresponding probabilities
///@param {bool} _return_index if true return selected index; if false [default] return value from _array
///@return {*} the randomly selected item or index
function array_random(_array = [], _probabilities = [], _return_index = false) {
// Specifying an empty _array means [0,1,...] the same size as _probs array
// Specifying an empty _probs means considering uniform probabilities the same size as _array
// If both are empty, generate a Bernoulli with p=0.5 (fair coin toss)
var _arr = _array;
var _probs = _probabilities;
var _n = array_length(_arr);
var _p = array_length(_probs);
if (!is_array(_arr) && !is_array(_probs) || _n == 0 && _p == 0) {
return choose(0,1);
}
else {
if (array_length(_arr) == 0) for (var _i=0; _i<_p; _i++) array_push(_arr, _i);
if (array_length(_probs) == 0) for (var _i=0; _i<_n; _i++) array_push(_probs, 1/_n);
_n = array_length(_arr);
_p = array_length(_probs);
if (_n != _p) throw("The value array and the probability array must be of the same size");
var _neg = false;
_i=0;
while (_i<_p && !_neg) {
if (_probs[_i] < 0) _neg = true;
else _i++;
}
if (_neg) throw("The probability array cannot have negative values");
// Normalize probability array
var _sum = 0;
for (var _i=0; _i<_p; _i++) _sum += _probs[_i];
if (abs(1-_sum) != 1) for (var _i=0; _i<_p; _i++) _probs[_i] /= _sum;
// Generate continuous random variable and compare against CDF
var _u = random(1);
var _i = 0;
var _cdf = _probs[0];
while (_u > _cdf && _i<_p) {
_i++;
_cdf += _probs[_i];
}
if (_return_index) return _i;
else return _arr[_i];
}
}
Let's try to use the above function to generate the random items mentioned above when the player opens a chest:
var _item = array_random(items, [0.4, 0.3, 0.2, 0.1], true);
You can interact with the following GameMaker app to observe a real-world example. Click on the chest a few times to open it and get an item each time. Scroll the loot list with mouse wheel or arrow keys, to view what you got each time. Then, you can click on the "Open 500 times" button to repeat the experiment. Watch the histogram to the right to understand how the distribution changes; after ~1,000 experiments or so, the distribution of drops should mimic the selected probabilities for the items. Click on the randomize button to restart the simulation (this will also change the PRNG seed).
As you can see, with this method we can create an arbitrarily complex distribution for our needs and use the same GameMaker function to simulate the corresponding random variables.
Some additional notes about the previous function. First, it lets you specify an empty array $A$ (in which case it will let you randomly select an index number $0$ to the length of $A$) or an empty probability array $P$ (in which case it will select an item from $A$ randomly with discrete uniform probability, akin to choose). Second, if the values in $P$ are nonnegative (the function will throw an exception if you have a negative value in $P$), but the values don't add up to 1, the function will also normalize them (i.e. convert them to values that add up to 1). This allows you to specify the probabilities as percentages (the usual way), 100-based integers or even relative weights. So, for example, the item selection in our previous example could have been specified as:
var _item = array_random(items, [4, 3, 2, 1], true);
This means that the gold is four times as likely as the sword, the potion is three times as likely, etc. This also allows you to think of your outcomes in terms of odds instead of probabilities, which can sometimes be more intuitive for some people. The odds of an outcome are defined as the probability of getting that outcome, divided by the probability of not getting it. For example, on our loot example, the odds of getting the sword are $0.1/0.9 = 1/9 = 1:9 \approx 0.111...$, whereas getting the gold has odds of $0.4/0.6 = 2/3 \approx 0.666...$.
In this level we have seen the basics of generating uniform numbers - either discrete or continuous, we have learned the secrets of the PRNG seed and we have seen a method of generating non-uniform discrete distributions. In the next level of the dungeon we'll check out some other probability distributions with sample applications. If you're ready then, let's...